第二节 顺序表的查找

1、一般顺序表的查找算法

（1）算法描述

int SeqSearch(SeqList R，KeyType k，int n)

｛　 //R[0]作为哨兵，用R[0].key==k作为循环下界的终结条件

　　R[0].key=k； 　　　　　//设置哨兵

　　i=n； 　　　　　　　　//从后向前扫描

　　while(R[i].key!=k)

　　　i- -；

　　return i； 　　　　　　//返回其下标，若找不到，返回0

｝

（2）算法分析

① 查找成功的情况：最好的情况比较1次，最坏的情况比较n次

　查找成功时的平均查找长度=（1+2+3+…+n）/n=

② 查找失败时的查找长度=（n+1）

③ 如果查找成功和不成功机会相等，顺序查找的平均查找长度为

（（n+1）/2+（n+1））/2= （n+1）

2、在递增有序的顺序表的查找算法

（1）算法描述

int SeqSearchl(SeqList R，KeyType k，int n)　　　　 //有序表的顺序查找算法

｛ 　int i=n；　　　　　　　　　　　　　　　　 //从后向前扫描，表按递增排序

　　while(R[i].key>k)

　　　　i--；　　　　　　　　　　　　　　　　 //循环结束时，要么R[i].key=k，要么R[i].key<k

　　if(R[i].key==k)

　　　return i；　　　　　　　　　　　　　　　 //找到，返回其下标

　　return 0； 　　　　　　　　　　　　　　　　//没找到，返回O

｝

（2）算法分析

①查找成功的平均查找长度=

②查找失败的平均查找长度=

③如果查找成功和不成功机会相等，该算法的平均查找长度为

对有序表可以用查找效率较高的二分查找方法来实现查找运算。

1、二分查找法的思想

二分查找的思想:首先将待查的k值和有序表R[1…n]的中间位置mid上的记录的关键字进行比较，若相等，则查找成功，返回该记录的下标mid；否则，若R[mid].key>k，则k在左子表R[1…mid-1]中，接着再在左子表中进行二分查找即可；否则，若R[mid].key<k，则说明待查记录在右子表R[mid+l…n]中，接着只要在右子表中进行二分查找即可。这样，经过一次关键字的比较，就可缩小一半的查找空间，如此进行下去，直到找到关键字为k的记录或者当前查找区间为空时(即查找失败)为止。二分查找的过程是递归的。

2、实例分析

3、算法描述

（1）二分查找递归算法

int BinSearch(SeqList R，KeyType k，int low，int high)

{ 　//在区间R[low...high]内进行二分递归，查找关键字值等于k的记录

　　//1ow的初始值为1，high的初始值为n

　 int mid；

　 if(low<=high)

　　{ mid=(low+high)／2；

　　　if (R[mid].key==k) return mid； 　　　　　　　//查找成功，返回其下标

　　　if (R[mid].key>k)

　　　　return BinSearch(R，k，low，mid-1) 　　　//在左子表中继续查找

　　　else

　　　　return BinSearch(R，k，mid+1，high) 　　//在右子表中继续查找

　　｝

　　else

　　　return 0；

｝

（2）二分查找非递归算法

int BinSearch(SeqLiSt R，KeyType k，int n) 　//初始化上下界

{　int low=l，mid，high=n；

　 while(low<=high)

　　 {mid=(low+high)／2；

　　　if( R[mid].key==k)

　　　　return mid； 　　　　　　　　　//查找成功，返回其下标

　　　if( R[mid].key>k)

　　　　high=mid-1；　　　　　　　　 //修改上界

　　　else low=mid+1；　　　　　　　 //修改下界

　　}

　　return 0；　　　　　　　　　　　 //查找失败，返回0值

}

4、算法分析

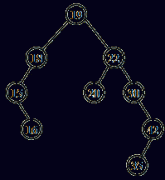
二分查找方法可以用一棵判定树描述，查找任一元素的过程对应该树中从根结点到相应结点的一条路径。最短的查找长度为1，最长的查找长度为对应判定树的深度 ，平均查找长度为 log₂（n+1）-1≈log₂（n+1）-1。二分查找方法效率高是有代价的，因为有序表是通过排序而得到的，而排序操作又是比较费时的。二分查找只适用于顺序结构上的有序表，对链式结构无法进行二分查找。

5、应用实例

【例】试写一算法，利用二分查找算法在有序表R中插入一个元素x，并保持表的有序性。

void BinInsert (SeqList R，KeyType x，InfoType y，int n)

{　int low=1，high=n，mid，inspace，i ；

　 int find=0；　　　　　　　　　　　　 //find是作为是否找到与x相等的关键字，先假设未发现

　 while (low<=high&&! find)

　　{mid=(low+high)／2；

　　if (x<R[mid].key) high=mid-1；

　　else if (x>R[mid].key) low=mid+1；

　　　else find=1；

　　}

　if(find)

　　inspace=mid；　　　　　　　　　　 //找到关键字与x相等，mid为x的插入位置

　else

　　inspace=low　　　　　　　　　　　 //所指向的结点关键字正好大于x，此时low即为插入位置

　for(i=n；i>=inspace；i--)

　　R[i+1]=R[i]； 　　　　　　　　　　//后移结点，留出插入的空位

　R[inspace].key=x；　　　　　　　　　 //插入结点，x是该结点的关键字，y是其他数据

　R[inspace].data=y；

}

三、索引顺序查找

索引顺序查找又称分块查找。它是一种性能介于顺序查找和二分查找之间的查找方法。

1、 索引查找表的存储结构

（1）"分块有序"的线性表

表R[1...n]均分为b块，前b-1块中结点个数为 ，第b块的结点数小于等于s；每一块中的关键字不一定有序，但前一块中的最大关键字必须小于后一块中的最小关键字，即表是"分块有序"的。

（2）索引表

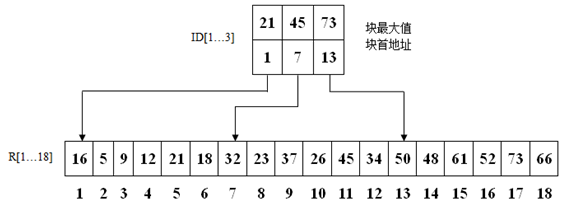
抽取各块中的最大关键字及其起始位置构成一个索引表ID[l…b]，即：ID[i](1≤i≤b)中存放第i块的最大关键字及该块在表R中的起始位置。由于表R是分块有序的，所以索引表是一个递增有序表。

【例】下图就是满足上述要求的存储结构，其中R只有18个结点，被分成3块，每块中有6个结点，第一块中最大关键字21小于第二块中最小关键字23，第二块中最大关键字45小于第三块中最小关键字48。

2、索引查找的基本思想

（1）首先查找索引表

索引表是有序表，可采用二分查找或顺序查找，以确定待查的结点在哪一块。

（2）然后在已确定的块中进行顺序查找

由于块内无序，只能用顺序查找。

3、索引查找的平均查找长度

（1）查找索引表采用二分查找时的平均查找长度

ASL_blk=log₂（b+1）-1+（s+1）/2≈log₂（n/s+1）+s/2

（2）查找索引表采用顺序查找时的平均查找长度

ASL_blk＝（b+1）/2＋（s+1）/2＝（b+s）/2+1＝（n/s+s）/2+1 =（块数+块长）/2+1

当s取 （即s=b）时， ASL_blk 达到最小值+1，即当采用顺序查找确定块时，应将各块中的结点数选定为。

四、三种查找方法比较

1、顺序查找

优点：算法简单，对表的存储结构无任何要求。

缺点：查找效率低，查找成功的平均查找长度为（n+1)／2，查找失败的查找长度为（n+1）。

2、二分查找

优点：二分查找的速度快，效率高，查找成功的平均查找长度约为log₂(n+1)-l。

缺点：要求表以顺序存储表示并且是按关键字有序，使用高效率的排序方法也要花费O(nlog₂n)的时间。另外，当对表结点进行插入或删除时，需要移动大量的元素，所以二分查找适用于表不易变动且又经常查找的情况。

3、分块查找

优点：在表中插入或删除一个记录时，只要找到该记录所属的块，就可以在该块内进行插入或删除运算。因为块内记录是无序的，所以插入或删除比较容易，无需移动大量记录。

缺点：是需要增加一个辅助数组的存储空间和将初始表块排序的运算，它也不适宜用链式存储结构。

此外，顺序查找、二分查找和分块查找三种查找算法的时间复杂度分别为：O(n)、O(log₂n)和O( )。分块查找算法的效率介于顺序查找和二分查找之间。

【例】若表中有10000个结点，则应把它分成100个块，每块中含100个结点。用顺序查找确定块，分块查找平均需要做 次比较；顺序查找平均需做（n+1）/2≈5000次比较；二分查找最多需 次比较，平均查找长度log₂10001-1。