第六节 - 拓扑排序
发布时间:2020-09-20 11:03来源:未知
第六节 拓扑排序
1、拓扑排序的概念
对一有向图,如果从Vi到Vj存在一条路径,且在由图中所有顶点构成的线性序列中,Vi总在Vj之前,那么这样的线性序列就被称为拓扑序列。构造一个有向图的拓扑序列的过程称为拓扑排序。
一个有向图必须满足两个条件才存在拓扑序列:
① 初始时有向图中必须至少有一个入度为0的顶点。
② 有向图中不存在回路。
满足以上两条的有向图称为AOV网
2、拓扑排序过程是:
① 从有向图中选择一个入度为0的顶点;
② 从有向图中将该顶点以及由该顶点发出的所有弧全部删除;
③ 重复上述过程,直到剩余的网中不再存在入度为0的顶点。
【例】
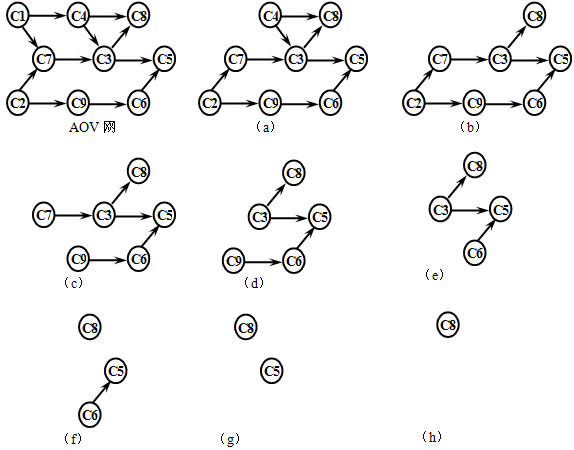
拓扑排序的结果为:C1,C4,C2,C7,C9,C3,C6,C5,C8
拓扑排序算法的时间复杂度为O(n+e)。
【真题选解】
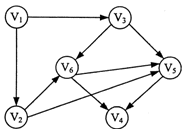
(例题•填空题)有向图G如图所示,它的两个拓扑排序序列分别为______和______。
本章小结
本章着重介绍了图的基本概念和一些重要的图结构上的运算。本章中的重点是:图的邻接矩阵和邻接表两种存储表示;图的深度优先搜素和广度优先搜索遍历算法、生成树和最小生成树以及Prim和Kruskal算法思想,并能够应用这些算法给出给定图的深度优先、广度优先遍历序列和构造最小生成树。
本章中还介绍了求最短路径的迪杰斯特拉(Dijkstra)算法和拓扑排序算法的基本思想,这些也是需要掌握和理解的内容。