第二节 - 图的存储结构
发布时间:2020-09-20 10:57来源:未知
第二节 图的存储结构
对于具有n个顶点的图,最常采用的存储方法有邻接矩阵存储方法与邻接表存储方法。
一、邻接矩阵表示法
1、邻接矩阵
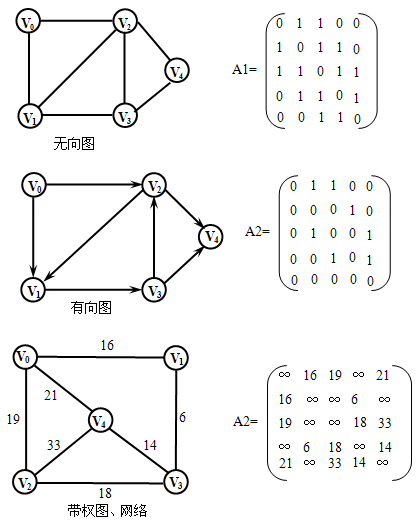
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下定义的n阶方阵:
![]()
【例】
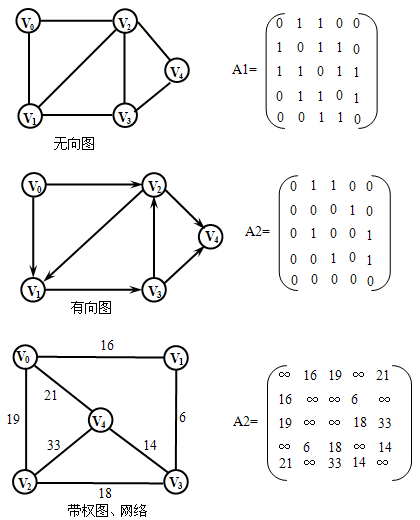
2、采用邻接矩阵存储方法具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,按照压缩存储的思想,在具体存放邻接矩阵时只需存放上(或者下)三角形阵的元素即可。
② 不带权的有向图的邻接矩阵一般来说是一个稀疏矩阵(特别是对于稀疏图),于是可以采用三元组表的方法存储邻接矩阵。
③ 对于无向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的度D(Vi)。
④ 对于有向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的出度OD(Vi)(或者入度ID(Vi))。
⑤ 对于无向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好是边数的2倍。
⑥ 对于有向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好等于弧数。
⑦ 一个图的邻接矩阵表示是唯一的。
【真题选解】
(例题•填空题)若无向图G中有n个顶点m条边,采用邻接矩阵存储,则该矩阵中非0元素的个数为___________。
3、邻接矩阵表示的存储结构定义
#define MaxVertexNum 50 //最大顶点数
typedef Struct
{ vertexTvpe vexs[MaxVertexNum]; //顶点数组,类型假定为char型
Adjmstrix arcs [MaxVertexNum][MaxVertexNum]; //邻接矩阵,假定为int型
}MGraph;
4、建立一个无向网的算法
【算法描述】
Void CreateMGraph(MGraph *G,int n,int e)
{ //采用邻接矩阵表示法构造无向网G,n、e表示图的当前顶点数和边数
int i,j,k,w;
scanf("%d,%d",&n,&e); //读入顶点数和边数
for(i=0;i<n;i++) //输入顶点信息
scanf("%c",&G->vexs[i]);
for(i=0; i<n;i++)
for(j=0;j<n; j++)
G->arcs[i][j]=INT_MAX; //初始化邻接矩阵元素为无穷大,一般填32767
for(k=0;k<e;k++) //读入e条边,建立邻接矩阵
//读入一条边的两端顶点序号i、j及边上的权W
{ scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
G->arcs[j][i]=w; //置矩阵对称元素权值
}
}
算法的时间复杂度O(n2)
二、邻接表表示法
1、邻接表
对于具有n个顶点的图建立n个线性链表。每一个链表最前面都分别设置一个称之为顶点表结点,n个顶点构成一个数组结构。第i个链表中的每一个链结点称之为边表结点。
【例】
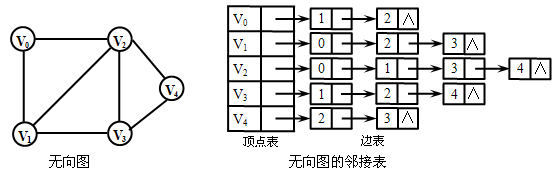
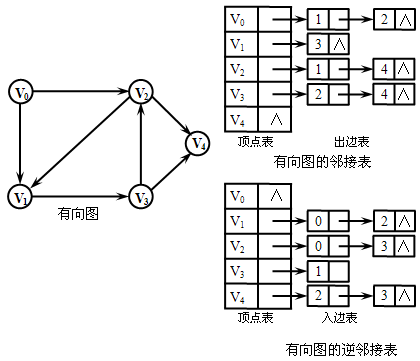
2、采用邻接表存储方法具有以下特点:
① 一个图的邻接表表示法不唯一,这是因为邻接表中各结点的链接次序取决于建立邻接表的算法(前插法还是后插法建链表)及边的输入次序。
② 对于无向图,若它有n个顶点,e条边,则其邻接表中需要2e+n个结点。其中有2e个边表结点,n个顶点表结点。边表结点的个数一定是偶数,为边数的2倍。
③ 对于有向图,若它有n个顶点,e条边,则其邻接表中需要e+n个结点。其中有e个边表结点,n个顶点表结点。
④ 对于无向图,第i个链表中的边表结点的数目是第i个顶点的度。
⑤ 对于有向图,第i个链表中的边表结点的数目是第i个顶点的出度。在其逆邻接表中,第i个链表中的边表结点的数目是第i个顶点的入度。
3、图的邻接表存储结构定义
#define MaxVertexNum 20
typedef char VertexType;
typedef struct node //边表结点类型
{ int adjvexj //顶点的序号
struct node *next; //指向下一条边的指针
}EdgeNode;
typedef struct vnode //顶点表结点
{ VertexType vertex; //顶点域
EdgeNode *link; //边表头指针
}VNode,Adjlist[MaxVertexNum]; //邻接表
typedef Adjlist ALGraph; //定义为图类型
4、无向图邻接表的建表算法:
void CreateGraph(ALGraph GL,int n,int e)
{ //n为顶点数,e为图的边数
int i,j,k;EdgeNode *p;
for(i=0;i<n;i++) //建立顶点表
{ GL[i].vertex=getchar(); //读入顶点信息
GL[i].1ink=NULL; //边表头指针置空
}
for(k=0;k<e;k++) //采用头插法建立每个顶点的邻接表
{ scanf("%d,%d",&i,&j); //读入边(vi,vj)的顶点序号
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adjvex=j; //将邻接点序号j赋给新结点的邻接点域
p->next=GL[i].1ink;
GL[i].1ink=p; //将新结点插入到顶点vi的边表头部
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adj.vex=i; //将邻接点序号i赋给新结点的邻接点域
p->next=GL[j].1ink;
GL[j].1ink=p; //将新结点插入到顶点vj的边表头部
}
}
算法的时间复杂度O(n+e)
建立有向图的邻接表更加简单,每当读入一个顶点对<i,j>时,仅需要生成一个邻接点序号为j的边表结点,将其插入到Vi的出边表头即可第二节 图的存储结构
对于具有n个顶点的图,最常采用的存储方法有邻接矩阵存储方法与邻接表存储方法。
一、邻接矩阵表示法
1、邻接矩阵
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下定义的n阶方阵:
![]()
【例】

2、采用邻接矩阵存储方法具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,按照压缩存储的思想,在具体存放邻接矩阵时只需存放上(或者下)三角形阵的元素即可。
② 不带权的有向图的邻接矩阵一般来说是一个稀疏矩阵(特别是对于稀疏图),于是可以采用三元组表的方法存储邻接矩阵。
③ 对于无向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的度D(Vi)。
④ 对于有向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的出度OD(Vi)(或者入度ID(Vi))。
⑤ 对于无向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好是边数的2倍。
⑥ 对于有向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好等于弧数。
⑦ 一个图的邻接矩阵表示是唯一的。
【真题选解】
(例题•填空题)若无向图G中有n个顶点m条边,采用邻接矩阵存储,则该矩阵中非0元素的个数为___________。
3、邻接矩阵表示的存储结构定义
#define MaxVertexNum 50 //最大顶点数
typedef Struct
{ vertexTvpe vexs[MaxVertexNum]; //顶点数组,类型假定为char型
Adjmstrix arcs [MaxVertexNum][MaxVertexNum]; //邻接矩阵,假定为int型
}MGraph;
4、建立一个无向网的算法
【算法描述】
Void CreateMGraph(MGraph *G,int n,int e)
{ //采用邻接矩阵表示法构造无向网G,n、e表示图的当前顶点数和边数
int i,j,k,w;
scanf("%d,%d",&n,&e); //读入顶点数和边数
for(i=0;i<n;i++) //输入顶点信息
scanf("%c",&G->vexs[i]);
for(i=0; i<n;i++)
for(j=0;j<n; j++)
G->arcs[i][j]=INT_MAX; //初始化邻接矩阵元素为无穷大,一般填32767
for(k=0;k<e;k++) //读入e条边,建立邻接矩阵
//读入一条边的两端顶点序号i、j及边上的权W
{ scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
G->arcs[j][i]=w; //置矩阵对称元素权值
}
}
算法的时间复杂度O(n2)
二、邻接表表示法
1、邻接表
对于具有n个顶点的图建立n个线性链表。每一个链表最前面都分别设置一个称之为顶点表结点,n个顶点构成一个数组结构。第i个链表中的每一个链结点称之为边表结点。
【例】


2、采用邻接表存储方法具有以下特点:
① 一个图的邻接表表示法不唯一,这是因为邻接表中各结点的链接次序取决于建立邻接表的算法(前插法还是后插法建链表)及边的输入次序。
② 对于无向图,若它有n个顶点,e条边,则其邻接表中需要2e+n个结点。其中有2e个边表结点,n个顶点表结点。边表结点的个数一定是偶数,为边数的2倍。
③ 对于有向图,若它有n个顶点,e条边,则其邻接表中需要e+n个结点。其中有e个边表结点,n个顶点表结点。
④ 对于无向图,第i个链表中的边表结点的数目是第i个顶点的度。
⑤ 对于有向图,第i个链表中的边表结点的数目是第i个顶点的出度。在其逆邻接表中,第i个链表中的边表结点的数目是第i个顶点的入度。
3、图的邻接表存储结构定义
#define MaxVertexNum 20
typedef char VertexType;
typedef struct node //边表结点类型
{ int adjvexj //顶点的序号
struct node *next; //指向下一条边的指针
}EdgeNode;
typedef struct vnode //顶点表结点
{ VertexType vertex; //顶点域
EdgeNode *link; //边表头指针
}VNode,Adjlist[MaxVertexNum]; //邻接表
typedef Adjlist ALGraph; //定义为图类型
4、无向图邻接表的建表算法:
void CreateGraph(ALGraph GL,int n,int e)
{ //n为顶点数,e为图的边数
int i,j,k;EdgeNode *p;
for(i=0;i<n;i++) //建立顶点表
{ GL[i].vertex=getchar(); //读入顶点信息
GL[i].1ink=NULL; //边表头指针置空
}
for(k=0;k<e;k++) //采用头插法建立每个顶点的邻接表
{ scanf("%d,%d",&i,&j); //读入边(vi,vj)的顶点序号
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adjvex=j; //将邻接点序号j赋给新结点的邻接点域
p->next=GL[i].1ink;
GL[i].1ink=p; //将新结点插入到顶点vi的边表头部
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adj.vex=i; //将邻接点序号i赋给新结点的邻接点域
p->next=GL[j].1ink;
GL[j].1ink=p; //将新结点插入到顶点vj的边表头部
}
}
算法的时间复杂度O(n+e)
建立有向图的邻接表更加简单,每当读入一个顶点对<i,j>时,仅需要生成一个邻接点序号为j的边表结点,将其插入到Vi的出边表头即可
对于具有n个顶点的图,最常采用的存储方法有邻接矩阵存储方法与邻接表存储方法。
一、邻接矩阵表示法
1、邻接矩阵
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下定义的n阶方阵:
![]()
【例】
2、采用邻接矩阵存储方法具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,按照压缩存储的思想,在具体存放邻接矩阵时只需存放上(或者下)三角形阵的元素即可。
② 不带权的有向图的邻接矩阵一般来说是一个稀疏矩阵(特别是对于稀疏图),于是可以采用三元组表的方法存储邻接矩阵。
③ 对于无向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的度D(Vi)。
④ 对于有向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的出度OD(Vi)(或者入度ID(Vi))。
⑤ 对于无向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好是边数的2倍。
⑥ 对于有向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好等于弧数。
⑦ 一个图的邻接矩阵表示是唯一的。
【真题选解】
(例题•填空题)若无向图G中有n个顶点m条边,采用邻接矩阵存储,则该矩阵中非0元素的个数为___________。
3、邻接矩阵表示的存储结构定义
#define MaxVertexNum 50 //最大顶点数
typedef Struct
{ vertexTvpe vexs[MaxVertexNum]; //顶点数组,类型假定为char型
Adjmstrix arcs [MaxVertexNum][MaxVertexNum]; //邻接矩阵,假定为int型
}MGraph;
4、建立一个无向网的算法
【算法描述】
Void CreateMGraph(MGraph *G,int n,int e)
{ //采用邻接矩阵表示法构造无向网G,n、e表示图的当前顶点数和边数
int i,j,k,w;
scanf("%d,%d",&n,&e); //读入顶点数和边数
for(i=0;i<n;i++) //输入顶点信息
scanf("%c",&G->vexs[i]);
for(i=0; i<n;i++)
for(j=0;j<n; j++)
G->arcs[i][j]=INT_MAX; //初始化邻接矩阵元素为无穷大,一般填32767
for(k=0;k<e;k++) //读入e条边,建立邻接矩阵
//读入一条边的两端顶点序号i、j及边上的权W
{ scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
G->arcs[j][i]=w; //置矩阵对称元素权值
}
}
算法的时间复杂度O(n2)
二、邻接表表示法
1、邻接表
对于具有n个顶点的图建立n个线性链表。每一个链表最前面都分别设置一个称之为顶点表结点,n个顶点构成一个数组结构。第i个链表中的每一个链结点称之为边表结点。
【例】
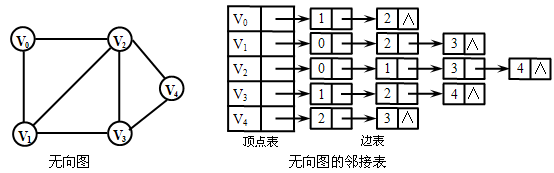
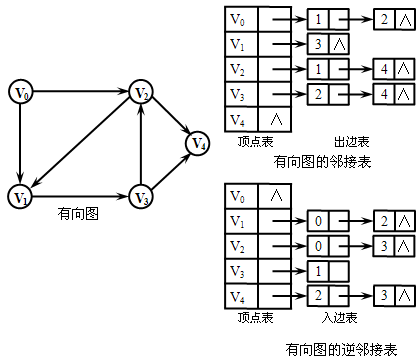
2、采用邻接表存储方法具有以下特点:
① 一个图的邻接表表示法不唯一,这是因为邻接表中各结点的链接次序取决于建立邻接表的算法(前插法还是后插法建链表)及边的输入次序。
② 对于无向图,若它有n个顶点,e条边,则其邻接表中需要2e+n个结点。其中有2e个边表结点,n个顶点表结点。边表结点的个数一定是偶数,为边数的2倍。
③ 对于有向图,若它有n个顶点,e条边,则其邻接表中需要e+n个结点。其中有e个边表结点,n个顶点表结点。
④ 对于无向图,第i个链表中的边表结点的数目是第i个顶点的度。
⑤ 对于有向图,第i个链表中的边表结点的数目是第i个顶点的出度。在其逆邻接表中,第i个链表中的边表结点的数目是第i个顶点的入度。
3、图的邻接表存储结构定义
#define MaxVertexNum 20
typedef char VertexType;
typedef struct node //边表结点类型
{ int adjvexj //顶点的序号
struct node *next; //指向下一条边的指针
}EdgeNode;
typedef struct vnode //顶点表结点
{ VertexType vertex; //顶点域
EdgeNode *link; //边表头指针
}VNode,Adjlist[MaxVertexNum]; //邻接表
typedef Adjlist ALGraph; //定义为图类型
4、无向图邻接表的建表算法:
void CreateGraph(ALGraph GL,int n,int e)
{ //n为顶点数,e为图的边数
int i,j,k;EdgeNode *p;
for(i=0;i<n;i++) //建立顶点表
{ GL[i].vertex=getchar(); //读入顶点信息
GL[i].1ink=NULL; //边表头指针置空
}
for(k=0;k<e;k++) //采用头插法建立每个顶点的邻接表
{ scanf("%d,%d",&i,&j); //读入边(vi,vj)的顶点序号
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adjvex=j; //将邻接点序号j赋给新结点的邻接点域
p->next=GL[i].1ink;
GL[i].1ink=p; //将新结点插入到顶点vi的边表头部
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adj.vex=i; //将邻接点序号i赋给新结点的邻接点域
p->next=GL[j].1ink;
GL[j].1ink=p; //将新结点插入到顶点vj的边表头部
}
}
算法的时间复杂度O(n+e)
建立有向图的邻接表更加简单,每当读入一个顶点对<i,j>时,仅需要生成一个邻接点序号为j的边表结点,将其插入到Vi的出边表头即可。
对于具有n个顶点的图,最常采用的存储方法有邻接矩阵存储方法与邻接表存储方法。
一、邻接矩阵表示法
1、邻接矩阵
设G=(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下定义的n阶方阵:
![]()
【例】

2、采用邻接矩阵存储方法具有以下特点:
① 无向图的邻接矩阵一定是一个对称矩阵。因此,按照压缩存储的思想,在具体存放邻接矩阵时只需存放上(或者下)三角形阵的元素即可。
② 不带权的有向图的邻接矩阵一般来说是一个稀疏矩阵(特别是对于稀疏图),于是可以采用三元组表的方法存储邻接矩阵。
③ 对于无向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的度D(Vi)。
④ 对于有向图,邻接矩阵的第i行(或者第i列)非零元素(或者非∞元素)的个数正好是第i个顶点的出度OD(Vi)(或者入度ID(Vi))。
⑤ 对于无向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好是边数的2倍。
⑥ 对于有向图,邻接矩阵的所有非零元素(或者非∞元素)的个数正好等于弧数。
⑦ 一个图的邻接矩阵表示是唯一的。
【真题选解】
(例题•填空题)若无向图G中有n个顶点m条边,采用邻接矩阵存储,则该矩阵中非0元素的个数为___________。
3、邻接矩阵表示的存储结构定义
#define MaxVertexNum 50 //最大顶点数
typedef Struct
{ vertexTvpe vexs[MaxVertexNum]; //顶点数组,类型假定为char型
Adjmstrix arcs [MaxVertexNum][MaxVertexNum]; //邻接矩阵,假定为int型
}MGraph;
4、建立一个无向网的算法
【算法描述】
Void CreateMGraph(MGraph *G,int n,int e)
{ //采用邻接矩阵表示法构造无向网G,n、e表示图的当前顶点数和边数
int i,j,k,w;
scanf("%d,%d",&n,&e); //读入顶点数和边数
for(i=0;i<n;i++) //输入顶点信息
scanf("%c",&G->vexs[i]);
for(i=0; i<n;i++)
for(j=0;j<n; j++)
G->arcs[i][j]=INT_MAX; //初始化邻接矩阵元素为无穷大,一般填32767
for(k=0;k<e;k++) //读入e条边,建立邻接矩阵
//读入一条边的两端顶点序号i、j及边上的权W
{ scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
G->arcs[j][i]=w; //置矩阵对称元素权值
}
}
算法的时间复杂度O(n2)
二、邻接表表示法
1、邻接表
对于具有n个顶点的图建立n个线性链表。每一个链表最前面都分别设置一个称之为顶点表结点,n个顶点构成一个数组结构。第i个链表中的每一个链结点称之为边表结点。
【例】


2、采用邻接表存储方法具有以下特点:
① 一个图的邻接表表示法不唯一,这是因为邻接表中各结点的链接次序取决于建立邻接表的算法(前插法还是后插法建链表)及边的输入次序。
② 对于无向图,若它有n个顶点,e条边,则其邻接表中需要2e+n个结点。其中有2e个边表结点,n个顶点表结点。边表结点的个数一定是偶数,为边数的2倍。
③ 对于有向图,若它有n个顶点,e条边,则其邻接表中需要e+n个结点。其中有e个边表结点,n个顶点表结点。
④ 对于无向图,第i个链表中的边表结点的数目是第i个顶点的度。
⑤ 对于有向图,第i个链表中的边表结点的数目是第i个顶点的出度。在其逆邻接表中,第i个链表中的边表结点的数目是第i个顶点的入度。
3、图的邻接表存储结构定义
#define MaxVertexNum 20
typedef char VertexType;
typedef struct node //边表结点类型
{ int adjvexj //顶点的序号
struct node *next; //指向下一条边的指针
}EdgeNode;
typedef struct vnode //顶点表结点
{ VertexType vertex; //顶点域
EdgeNode *link; //边表头指针
}VNode,Adjlist[MaxVertexNum]; //邻接表
typedef Adjlist ALGraph; //定义为图类型
4、无向图邻接表的建表算法:
void CreateGraph(ALGraph GL,int n,int e)
{ //n为顶点数,e为图的边数
int i,j,k;EdgeNode *p;
for(i=0;i<n;i++) //建立顶点表
{ GL[i].vertex=getchar(); //读入顶点信息
GL[i].1ink=NULL; //边表头指针置空
}
for(k=0;k<e;k++) //采用头插法建立每个顶点的邻接表
{ scanf("%d,%d",&i,&j); //读入边(vi,vj)的顶点序号
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adjvex=j; //将邻接点序号j赋给新结点的邻接点域
p->next=GL[i].1ink;
GL[i].1ink=p; //将新结点插入到顶点vi的边表头部
p=(EdgeNode*)malloc(sizeof(EdgeNode));
//生成新的边表结点
p->adj.vex=i; //将邻接点序号i赋给新结点的邻接点域
p->next=GL[j].1ink;
GL[j].1ink=p; //将新结点插入到顶点vj的边表头部
}
}
算法的时间复杂度O(n+e)
建立有向图的邻接表更加简单,每当读入一个顶点对<i,j>时,仅需要生成一个邻接点序号为j的边表结点,将其插入到Vi的出边表头即可。