第三节 - 队列(一)
发布时间:2020-09-20 10:40来源:未知
第三节 队列(一)
一、队列的定义及其运算
1、队列的定义
队列(Oueue)是一种操作受限的线性表,它只允许在表的一端进行元素插入,而在另一端进行元素删除。允许插入的一端称为队尾(rear),允许删除的一端称为队头(front)。新插入的结点只能添加到队尾,被删除的只能是排在队头的结点,因此,队列又称为先进先出(First In First Out)的线性表,简称为FIFO表。
【真题选解】某队列初始为空,若它的输入序列为(a,b,c,d),它的输出序列应为 ( )。
A.a,b,c,d B.d,c,b,a
C.a,c,b,d D.d,a,c,b
2、队列的基本运算
(1)置空队列InitQueue(Q),构造一个空队列。
(2)判队空QueueEmpty(Q),若Q为空队列,则返回TRUE,否则返回FALSE。
(3)入队列En(jueue(Q,x),若队列不满,则将数据x插入到Q的队尾。
(4)出队列DeQueue(Q),若队列不空,则删除队头元素,并返回该元素。
(5)取队头GetFront(Q),若队列不空,则返回队头元素。
二、顺序循环队列
1、顺序队列的概念
队列的顺序存储结构称为顺序队列。队列的顺序存储结构是利用一块连续的存储单元存放队列中的元素的,设置两个指针front和rear分别指示队头和队尾元素在表中的位置。
【例】设有一顺序队列Q,容量为5,初始状态时Q.front=Q.rear=0,画出做完下列操作后队列及其头尾指针的状态变化情况,若不能入队,请简述其理。
(1) d,e,b入队
(2) d,e出队
(3) i,j入队
(4) b出队
(5) n,o,p入队
【解答】队列及其头尾指针的状态变化情况如图所示
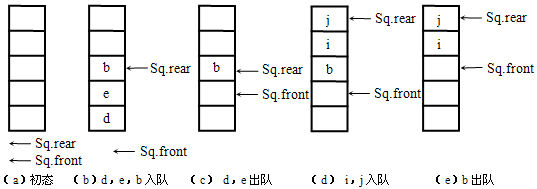
第(5)步操作无法进行,因队列已满,再有元素入队,就会溢出,发生假溢。
2、顺序循环队
为了解决顺序队的"假溢"问题采用循环队。约定循环队的队头指针指向队头元素在数组中实际位置的前一个位置,队尾指针指示队尾元素在数组中的实际位置。其次再约定队头指针指示的结点不用于存储队列元素,只起标志作用。这样当队尾指针"绕一圈"后赶上队头指针时视为队满。
【例】设Q是一个有11个元素存储空间的顺序循环队列,初始状态Q.front=Q.rear=0,写出下列操作后头、尾指针的变化情况,若不能入队,请说明理由。
d,e,b,g,h入队;d,e出队;
i,j,k,l,m入队;b出队;
n,o,p,q,r入队
【解答】
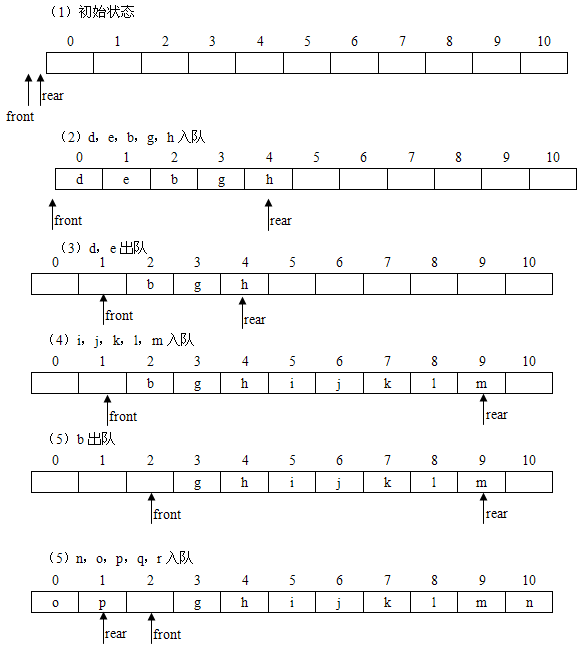
注意:p入队以后,队列就满了,不能再入队了,此时队列中的元素个数为10个(数组长度是11)
总结:队中元素个数: 
两种情况合并为:(QueueSize +rear-front)% QueueSize;
【真题选解】
设循环队列的容量为50(序号从0到49),现经过一系列的入队和出队运算后,有①front=11,rear=29;②front=29,rear=11;在这两种情况下,循环队列中的元素个数分别是______和______。
3、循环队的顺序存储的类型定义
#define QueLleSize 100
typedef char DataType; //假设数据为字符型
typedef struct
{ DataType data[QueueSize];
int front,rear;
}CirQueue;
4、循环队列基本运算的各算法
(1)置空队列
void InitQueue(CirQueue * Q )
{ Q->front=Q->rear=0 ;
}
(2)判队空
int QueueEmpty(CirQueue*Q)
{
return Q->rear==Q->front;
}
(3)判队满
int QueueFull(CirQueue*Q)
{
return(Q->rear+1)%QueueSize==Q->front;
}
(4)入队列
void EnQueue(CirQueue*Q,DataType x)
{ //插入元素x为队列Q新的队尾元素
if(QueueFull(Q))
printf("Queue overflow");
e1se
{ Q->data[Q->rear]=x;
Q->ear=(Q->rear+1)%QueueSize; //循环意义下的加1
}
}
(5)取队头元素
DataType GetFront(Ci rQueue*Q)
{ //获取Q的队头元素值
if(QueueEmpty(Q))
{ printf("Queue empty");
exit(0);}
else
return Q->data[Q->front]j
}
(6)出队列
DataType DeQueue(CirQueue*Q)
{ //删除Q的队头元素,并返回其值
DataType x;
if(QueueEmpty(Q))
{ printf("Queue empty");
exit(0);
}
else
{ x=Q->data[Q->front]; //保存待删除元素值
Q->front=(Q->front+1)%QueueSize; //头指针加1
return x; //返回删除元素值
}
}
【例】设栈S=(1,2,3,4,5,6,7),其中7为栈顶元素。请写出调用函数Algo(S)后栈S的状态。其函数为:
void Algo(SeqStack S)
{ int i=l;
CirQueue Q;SeqStack T; //定义一个循环队列和一个栈
InitQueue(&Q); Initstack(&T); //初始化队列和栈
while(!StackEmpty(&S))
{if(i%2!=0)
Push(&T,Pop(&S)); //栈中序号为奇数的元素入T栈中
//7、5、3、1顺序入栈T。
else
EnQueue(&Q, Pop(&S)); //序号为偶数的元素入队列Q中
//6、4、2顺序入队Q。
i++;
}
while(!QueueEmpty(&Q))
Push(&S,DeQueue(&Q)); //队Q中6、4、2顺序出队并入栈S
while(!StackEmpty(&T))
Push(&S,Pop(&T)); //队栈T中按1、3、5、7顺序出栈并入栈S
}
最后栈S中的元素为(6、4、2、1、3、5、7)。
三、链队
1、链队的定义
队列的链式存储结构称为链队列。它是一种限制在表头删除和表尾插入操作的单链表。
2、链队的数据类型定义
typedef struct qnode
{ DataType data ;
struct qnode *next;
}QueueNode;
typedef struct
{ QueueNode * front; //队头指针
QueueNode *rear; //队尾指针
}LinkQueue;
LinkQueue Q;

3、链队的基本运算实现
(1)构造空队列
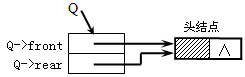
void InitQueue(LinkQueue *Q)
{
Q->front=(QueueNode *)malloc(sizeof(QueueNode)); //申请头结点
Q->rear=Q->front; //尾指针也指向头结点
Q->rear->next=NULL;
)
(2)判队空
int QueueEmpty(LinkQueue *Q)
{
return Q->rear==Q->front; //头尾指针相等队列为空
)
(3)入队列

void EnQueue(LinkQueue *Q,DataType x)
{ //将元素x插入链队列尾部
QueueNode *p=(QueueNode *)malloc(Sizeof(QueueNode)); //申请新结点
p->data=x ;
p->next=NULL;
Q->rear->next=p; //*p链到原队尾结点之后
Q->rear=p; //队尾指针指向新的队尾结点
}
(4)取队头元素
DataType GetFront(LinkQueue *Q)
{ //取链队列的队头元素值
if(QueueEmpty(Q)) //判队空
{printf("Queue underflow");
exit(0); //出错退出处理
}
else
return Q->front->next->data; //返回原队头元素值
)
(5)出队列
链队列的出队操作有两种不同情况要分别考虑。
①当队列的长度大于1时,则出队操作只需要修改头结点的指针域即可,尾指针不变,类似于单链表删除首结点,操作步骤:
s=Q->front->next;
Q->fron->next=s->next;
x=s->data;
free(s);return x; //释放队头结点,并返回其值
②若列队长度等于l,则出队时不仅要修改头结点指针域,而且还需要修改尾指针。
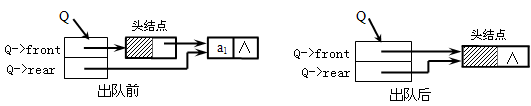
s=Q->front->next;
Q->front->next=NULL; //修队头指针
Q->rear=Q->front; //修改尾指针
x=s->data;
free(s); return x; //释放队头结点,并返回其值
为了方便,直接删除头结点,将原队头结点当头结点使,这样算法就简单了。

链队列的出队算法描述
DataType DeQueue(LinkQueue *Q)
{ //删除链队列的头结点,并返回头结点的元素值
QueueNode *P;
if(QueueEmpty(Q))
{printf("Queue underflow");
exit(0); //出错退出处理
}
else
{p=Q->front; //p指向头结点
Q->front=Q->front->next; //头指针指向原队头结点
free(p); //删除释放原头结点
return(Q->front->data); //返回原队头结点的数据值
}
}
【真题选解】算法f31的功能是清空带头结点的链队列Q.请在空缺处填入合适的内容,使其成为一个完整的算法.
typedef struct node
{ DataType data;
struct node *next;
}QueueNode;
typedef struct
{ QueueNode *front;//队头指针
QueueNode *rear;//队尾指针
}LinkQueue;
void f 31(LinkQueue*Q)
{ QueueNode*p,*s;
p= (1) ;
while(p!=NULL)
{ s=p;
p=p->next;
free (s);
}
________(2) =NULL;
Q->rear=_______(3)_______;
}
(1)__________________________________________
(2)__________________________________________
(3)__________________________________________
4、循环链队列

循环链队列的类型定义
typedef struct queuenode
{ DataType data;
struct queuenode *next;
}QueueNode;
QuelaeNode *rear;
(1)初始化空队列
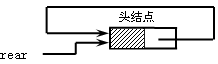
QueueNode *InitQueue(QueueNode *rear)
{ tear=(QueueNode *)malloc(sizeof(QueueNode)); //申请头结点
rear->next=rear;
return rear;
}
(2)入队列

void EnQueue(QueueNode *rear,Datatype x)
{ QueueNode *s=(QueueNode *)malloc(sizeof(QueueNode)); //申请新结点
s->data=x:
s->next=rear->next;
rear->next=s;
rear=s;
}
(3)出队列

DataType DelQueue(QueueNode *rear)
{ QueueNode *s,*t;
DataType x;
if ( rear->next==rear) //判队空
{printf ("Queue Empty");
exit(0);
}
else
{ s=rear->next; //s指向头结点
rear->next=s->next; //删除头结点
t=s->next; //t指向原队头结点
x=t->data; //保存原队头结点数据
free(s); //释放被删除的原头结点
return x; //返回出队结点的数据
}